Cualquiera sabe que, partiendo sólo de área de un rectángulo=base x altura, es muy fácil obtener el área de figuras planas poligonales: así salen el área de un paralelogramo, triángulo, trapecio, etc. Sólo se trata de cortar y acomodar pedazos (Por ejemplo). Pero cuando se trata de figuras con curvas, la cosa se complica. No parece fácil recortar un círculo para obtener un cuadrado; tiene que ver con la «cuadratura del círculo», cosa proverbialmente imposible. Sin embargo, el área de un círculo puede obtenerse por procedimientos especiales; acá vimos uno, que esencialmente hace corresponder el círculo a un triángulo de igual área.
Si ahora pasamos a superficies no planas, la cosa se complica aún más.
Imaginemos una pelota metida (justo) en una caja cilíndrica. ¿Qué tiene más superficie? ¿La pelota o la pared lateral del cilindro? Vale la pena detenerse a pensarlo.
Mostraremos que:
1. El área de la esfera y el área lateral del cilindro (es decir, el cilindro sin las tapas) son iguales.
2. El área de la tapa del cilindro (un círculo) es la cuarta parte del área lateral (y por lo tanto, también de la esfera)
Vamos a lo primero, que es lo más difícil. Imaginemos la esfera dentro del cilindro, e imaginemos que serruchamos todo con cortes horizontales, equiespaciados (llamemos h a la distancia vertical).
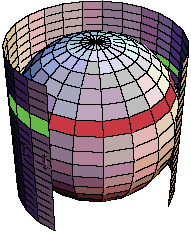 La imagen (sacada de acá;
el cilindro se muestra incompleto, para que se vea la esfera)
debería ayudar a entender.
La imagen (sacada de acá;
el cilindro se muestra incompleto, para que se vea la esfera)
debería ayudar a entender.Sobre el cilindro, quedan «cintas», todas iguales, de alto h; la verde, por ejemplo.
Sobre la esfera, quedan otras tantas cintas (como la roja). Las cintas sobre el cilindro y sobre la esfera coinciden cuando estamos sobre el «ecuador»; pero, a medida que subimos hacia el «polo», como el radio de circulo seccionado disminuye, la cinta sobre la esfera se irá acortando. Pero a su vez, como la cinta está cada vez más «inclinada», su altura será mayor. (No sigan leyendo si no entendieron lo anterior).
Demostremos que un efecto compensa el otro, y el área de cada cinta sobre la esfera es «casi» igual a la de la cinta sobre el cilindro (y ya veremos lo del «casi»).
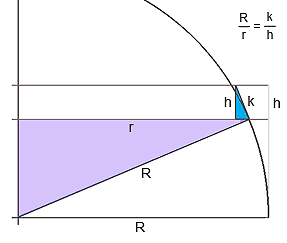 La figura siguiente, representa una sección vertical. Las líneas horizontales, separadas en h representan los planos
de corte horizontal. Sobre la esfera, de radio R,
queda una «cinta» curvada, de altura mayor que h. Suponiendo que h es
pequeña, aproximemos esta sección de la cinta por el segmento
k, tangente a la esfera; y llamemos r al «radio
pequeño», el que corresponde al círculo seccionado.
No es difícil ver que los triángulos sombreados en celeste y en violeta,
ambos rectángulos, son semejantes; por lo cual sus lados están en relación proporcional, como dice la figura. Entonces, lo que
la cinta se reduce en largo (r en lugar de R) se compensa exactamente con el aumento de altura (k en lugar de h). Ergo, la cinta sobre el cilindro tiene igual área a la cinta correspondiente sobre la esfera. Ergo, ambas áreas son iguales.
La figura siguiente, representa una sección vertical. Las líneas horizontales, separadas en h representan los planos
de corte horizontal. Sobre la esfera, de radio R,
queda una «cinta» curvada, de altura mayor que h. Suponiendo que h es
pequeña, aproximemos esta sección de la cinta por el segmento
k, tangente a la esfera; y llamemos r al «radio
pequeño», el que corresponde al círculo seccionado.
No es difícil ver que los triángulos sombreados en celeste y en violeta,
ambos rectángulos, son semejantes; por lo cual sus lados están en relación proporcional, como dice la figura. Entonces, lo que
la cinta se reduce en largo (r en lugar de R) se compensa exactamente con el aumento de altura (k en lugar de h). Ergo, la cinta sobre el cilindro tiene igual área a la cinta correspondiente sobre la esfera. Ergo, ambas áreas son iguales.
«Casi» iguales, en realidad, porque aproximamos la cinta curvada a un segmento. Pero esta aproximación mejora cuando h se hace cada vez más pequeña.
Para demostrar ahora que el área lateral del cilindro es cuatro veces la del círculo que forma la tapa (siempre sin usar conocimientos de cálculo, y sin necesidad de conocer pi): basta con imaginar el cilindro desplejado, como un rectángulo de alto R y ancho igual al perímetro del círculo. Comparando con esta figura, vemos que el triángulo -de área igual al círculo- entra cuatro veces en ese rectángulo.
QED. (Que es lo que queríamos demostrar).
Tenemos pues que el area de una esfera es cuatro veces el área del círculo de igual radio. Resultado nada obvio, y que Arquímedes supo (dicen que los egipcios lo madrugaron, pero no es seguro).
¿Y qué importancia tiene esto? Digo, no conocer el resultado (que seguramente tendrá «aplicaciones prácticas»; pero que puedo encontrar en cualquier manual de fórmulas geométricas), sino entender esta demostración. Bueno… es una forma de aprehender una verdad inmutable. Una verdad (y una forma de aprehenderla) meramente matemática, sí. Pero una verdad al fin. Y el que no entiende el placer, la impresión estética que una tal demostración produce en el que la comprende, no sabe lo que es la matemática.
Bueno, no me pierdo gran cosa, me dirá alguno. No sé, no sé.