Tenemos una habitación rectangular, con una pared
más larga que la otra, y altura igual al largo de la pared corta.
Digamos: 5m x 3m x 3m (pero por ahora las dimensiones exactas no importan) En la mitad de una pared corta, junto al piso, está la entrada de una ratonera. En la mitad de la otra pared, y cerca del techo, hay una araña; la araña quiere aprovechar que el ratón no está a la vista para asomarse a la cueva y picotear algún resto de comida; ella puede caminar por las paredes (y techo y piso), indistintamente
¿Cuál es el camino más corto que puede seguir?
A primera vista nos parece (¿no?) que lo más corto es bajar por la pared y atravesar el piso (camino marcado en verde).
¿Es así? ¿Depende de cuán larga sea la pared larga?
Para verlo, no hace falta mucha matemática; teorema de Pitágoras y no mucho más.
La solución, apretando el link.
La clave es pensar la habitación (paredes, techo y piso) «desplegada», como una caja de cartón, y dibujar la trayectoria en el plano resultante.
Claro que la trayectoria más corta será una recta, pero
hay diversas maneras de desplegar una caja,
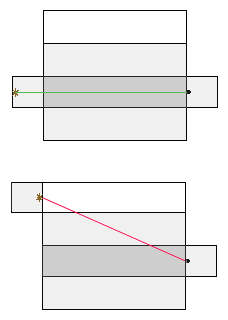
así que debemos ver las alternativas. La primer figura (el techo blanco, el piso de gris más oscuro que las paredes) es la opción más directa. En verde está la trayectoria «trivial». Y parece la trayectoria más corta, nomás.
Pero también podemos desplegarla según la segunda figura. Y encontramos la trayectoria roja, cruzando en diagonal techo, pared lateral y piso.
¿Cuál es más corta? No es muy evidente. Pero resulta que, si las paredes laterales son lo suficientemente largas (un 50% más largas que las paredes cortas, si la araña arranca pegada al techo) la trayectoria roja es la más corta.
La solución, evidentemente no cambia si la araña está algo (no mucho) alejada del techo. Pero así resulta aún más difícil de creer: para mí, al menos, resulta algo paradójico que el camino más corto arranque en este caso subiendo hacia el techo, alejándose del destino.
Otra variante, en este caso no para acentuar la paradoja sino más bien para hacer más plausible la solución, es imaginar la habitación como un cilindro acostado. Acá resulta más fácil «ver» la solución, como una hélice.
Otra vuelta de tuerca: puede uno plantear otro despliegue, intermedio entre los dos dados, que resulta en una trayectoria también oblicua pero empezando por la pared lateral, sin pasar por el techo. Puede demostrarse que esta alternativa no es mejor a la trayectoria roja… salvo para algún rango estrecho de distancias (con la araña alejada del techo).