Me acerca una matématica argentina radicada en Uruguay una solución
geométrica y muy sencilla al problem aquel.
Se agradece.
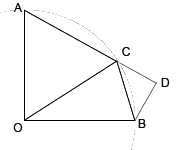
Primera observación: el ángulo ACB mide 180° – 45° = 135°. (La suma de los cuatro ángulos interiores del cuadrilátero OACB es 360°; además el ángulo en O es recto, los triángulos OAC y OCB son isósceles ; etc).
Ahora prolongamos AC hasta el punto D, de manera que CDB sea ángulo recto. Como ángulo(BCD)=45°, el triángulo BCD es rectángulo e isósceles. (CD = DB = CB / √2 )
Aplicamos teorema de Pitágoras al triángulo (no dibujado) ADB:
AB2 = (AC+CD)2 + DB2
Desarrollando el cuadrado, usando la identidad anterior resulta:
AB2 =AC2 + √2 AC CB + CB2
Y la incógnita (el radio del círculo) es r = OA = AB/√2.
De modo que la solución sale de:
r2 = (AC2+CB2)/2 + AC CB/√2
Mucho más sencillo y elegante que usar trigonometría. Es interesante notar que, aunque el planteo del problema es lógicamente «simétrico» respecto de los dos datos (y la solución, por supuesto, también lo es) la construcción y la fórmula intermedia no lo es (alternativamente, podríamos haber optado por prolongar el lado CB).
Ya que estamos ¿alguno sabe -pregunto- cómo hizo Arquímedes para deducir que la superficie de una esfera es cuatro veces el área del círculo máximo inscripto?