Recuerdo que en primer año del secundario (12 años) mi profesor de matemáticas (el gordo Bianco; buen profesor) me vio garabateando… para matar el tiempo, en lugar de dedicarme a cosas propias de mi edad y mi ambiente, estaba yo tratando de demostrar el teorema de Pitágoras. Un espanto. Una vergüenza, entre tantas. Mucho tiempo después, me dijeron que Einstein a esa edad hizo lo mismo; lo cual (aun suponiendo que no sea falso, como casi todas las anécdotas y dichos que se le atribuyen) no me consuela: porque él lo demostró, yo no (Y además, no tengo especial interés en parecerme a Einstein).
En la misma página, hay 54 demostraciones del teorema de Pitágoras. Mi profesor me salió con la 9, que será todo lo elegante que quieran, pero no es lo que andaba buscando. Para mí, la demostración es la 6.
Este fin de semana estuve dando vueltas con un problema que leí por ahí… Me hirió el orgullo no poder resolverlo con facilidad; pero después descubrí que había leído mal el enunciado.
 En mi versión, más difícil, el problema se reduce a calcular
el radio de un círculo en función de dos cuerdas consecutivas
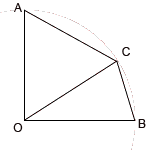
que subtienden un cuarto de circunferencia. Es más fácil verlo:
se trata de calcular OA (=OB=OC) dados AC y CB.
En mi versión, más difícil, el problema se reduce a calcular
el radio de un círculo en función de dos cuerdas consecutivas
que subtienden un cuarto de circunferencia. Es más fácil verlo:
se trata de calcular OA (=OB=OC) dados AC y CB.Agradeceré si alguno puede encontrar una solución geométrica. Es claro que sale con trigonometría pero debe haber algo más elegante.
(Creo que también debería salir igualando sumas de superficies de triángulos : S(OAB)+S(ABC)=S(OAC)+S(SCB) –fórmula de Herón mediante- y despejando la única incógnita, pero el álgebra pinta aburridísima).